Cómo manejar números enteros: 9 consejos útiles

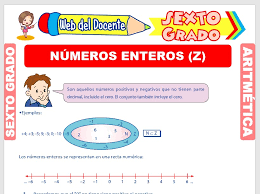
Los Números Enteros son un tipo de números que se caracterizan por ser los números naturales y sus opuestos. Estos números se representan con una línea recta, donde los números positivos están a la derecha de cero y los negativos a su izquierda.

Los Números Enteros incluyen a los números naturales (1, 2, 3, 4, etc.), los enteros negativos (-1, -2, -3, etc.) y el cero (0). Estas son las únicas cantidades en las que no hay fracciones ni decimales.

Todas las operaciones matemáticas se pueden realizar con Número Entero: adición (+), sustracción (-), multiplicación (*) y división (/). Muchas veces se usan para representar cantidades discretas o métricas como el tiempo o el dinero.

Los Número Entero también se utilizan en la programación de computadoras para controlar la ejecución de un programa. Por ejemplo, el lenguaje C usa enteros para controlar la ejecución de bucles (comandos repetitivos) o para realizar operaciones aritméticas simples.

En resumen, los Número Entero son un tipo fundamental de número en matemáticas y computación. Son usados para representar cantidades discretas o métricas sin fracciones ni decimales y son clave para la programación de computadoras.

9 consejos sobre números enteros

1. Practica con ejercicios para mejorar tus habilidades con los números enteros.
2. Recuerda que los números enteros pueden ser positivos o negativos.
3. Utiliza la regla de la multiplicación para simplificar operaciones con números enteros.
4. Aprende a identificar y utilizar fracciones equivalentes para resolver problemas de número entero más fácilmente.
5. Comprende el concepto de divisibilidad para determinar si un número es entero o no .
6. Utiliza propiedades como la asociativa, distributiva y conmutativa para simplificar operaciones con números enteros .
7. Resuelve problemas de ecuaciones lineales usando métodos algebraicos adecuados .
8. Estudia las leyes de los exponentes y cómo se relacionan con los números enteros .
9. Practica la división sintética para dividir grandes cantidades por pequeñas cantidades en forma rápida y sencilla .

Practica con ejercicios para mejorar tus habilidades con los números enteros.

¡Aprender sobre números enteros puede ser divertido y útil! Practicar con ejercicios es una excelente manera de mejorar tus habilidades con los números enteros. Esto te ayudará a comprender mejor los conceptos básicos de los números enteros, como la adición, la sustracción, la multiplicación y la división. Además, te dará más confianza para resolver problemas matemáticos más avanzados.

Hay muchas formas diferentes en las que puedes practicar con ejercicios de números enteros. Puedes encontrar libros de ejercicios específicamente diseñados para ayudarte a mejorar tus habilidades en este área. También hay muchas aplicaciones y sitios web que ofrecen prácticas interactivas en línea para que puedas aprender sobre los números enteros mientras te diviertes.

Para obtener los mejores resultados al practicar con ejercicios de números enteros, debes tratar de hacer una variedad de problemas diferentes. Esto te ayudará a desarrollar una comprensión sólida de todos los conceptos relacionados con los números enteros y te permitirá abordarlos con confianza cuando se presenten en situaciones reales. Así que ¡manos a la obra! ¡Practica tus habilidades con los números enteros!

Recuerda que los números enteros pueden ser positivos o negativos.

Los números enteros son un tipo de número muy importante para entender la matemática. Estos números se caracterizan porque no tienen fracciones ni decimales. Los números enteros pueden ser positivos o negativos. Los números positivos son aquellos mayores que cero, como 1, 2, 3, etc. Los números negativos son aquellos menores que cero, como -1, -2, -3, etc.

Es importante recordar que los números enteros pueden ser positivos o negativos y que esta distinción es fundamental para comprender la matemática. Por ejemplo, cuando se realizan operaciones con estas dos clases de número se obtienen resultados diferentes. Por lo tanto, es importante entender la diferencia entre los dos tipos de número para realizar operaciones matemáticas correctamente.

Utiliza la regla de la multiplicación para simplificar operaciones con números enteros.

La regla de la multiplicación es una herramienta útil para simplificar operaciones con números enteros. Esta regla nos dice que cuando se multiplican dos números enteros, el resultado es igual al producto de sus factores. Por ejemplo, si multiplicamos 4 y 5, el resultado es igual a 20 (4 x 5 = 20). Esto significa que podemos simplificar operaciones con números enteros al usar la regla de la multiplicación. Por ejemplo, en lugar de restar 8 y 2 para obtener 6 (8 – 2 = 6), podemos multiplicar 8 por -1 y luego sumarlo a 2 para obtener 6 (8 x (-1) + 2 = 6). Usando la regla de la multiplicación, podemos simplificar operaciones con números enteros y hacerlas más fáciles de realizar.

Aprende a identificar y utilizar fracciones equivalentes para resolver problemas de número entero más fácilmente.

Aprender a trabajar con números enteros puede ser un desafío para muchos estudiantes. Sin embargo, hay algunas herramientas útiles que pueden ayudar a simplificar el proceso. Una de ellas es aprender a identificar y utilizar fracciones equivalentes para resolver problemas de número entero.

Las fracciones equivalentes son aquellas que tienen el mismo valor numérico, pero diferente forma. Por ejemplo, 1/2 y 2/4 son fracciones equivalentes porque ambas representan la misma cantidad (1/2 = 0.5 = 2/4 = 0.5). Esta herramienta es útil para resolver problemas de números enteros porque permite simplificar los cálculos necesarios para encontrar la respuesta correcta. Por ejemplo, si se tiene un problema como «¿cuántos tercios hay en dos enteros?», se puede dividir la cantidad total (dos) entre la fracción equivalente (3/6), lo que resulta en 4 tercios.

En conclusión, utilizar fracciones equivalentes para resolver problemas de número entero puede ser una herramienta muy útil para los estudiantes que quieren aprender a trabajar con números enteros de manera eficiente y sencilla.

Comprende el concepto de divisibilidad para determinar si un número es entero o no .

El concepto de divisibilidad es un concepto importante que se debe comprender para determinar si un número es entero o no. Un número entero es aquel que se puede dividir exactamente por otro número sin dejar restos. Esto significa que el cociente y el resto deben ser ambos iguales a cero. Por ejemplo, si dividimos 8 entre 4, el cociente será 2 y el resto 0. Esta es una buena manera de determinar si un número es entero o no. Si un número no se puede dividir exactamente por otro, entonces no es un número entero. Por lo tanto, comprender el concepto de divisibilidad es la clave para saber si un número es entero o no.

Utiliza propiedades como la asociativa, distributiva y conmutativa para simplificar operaciones con números enteros .

Los números enteros son una parte importante de la matemática y hay muchas propiedades que se pueden usar para simplificar operaciones con estos números. Una de estas propiedades es la asociativa, que significa que el orden de los números no importa cuando se realizan operaciones. Por ejemplo, (3 + 4) + 5 = 3 + (4 + 5). Esto significa que puedes agrupar los números como quieras para simplificar las operaciones.

Otra propiedad útil es la conmutativa, lo que significa que el orden en el cual se realizan las operaciones no importa. Por ejemplo, 3 + 4 = 4 + 3. Esto ayuda a simplificar las operaciones ya que puedes reorganizar los números como quieras sin cambiar el resultado final.

Finalmente, hay la propiedad distributiva, lo que significa que cuando hay un número multiplicado por un grupo de números, puedes multiplicar cada miembro del grupo por ese número. Por ejemplo, 2 * (3 + 4) = 2 * 3 + 2 * 4. Esta propiedad también ayuda a simplificar las operaciones con números enteros al permitirte dividir y conquistar grandes problemas en problemas más pequeños y manejables.

En resumen, utilizando estas tres propiedades: asociativa, conmutativa y distributiva; puedes simplificar grandes problemas matemáticos usando números enteros al reorganizarlos y dividirlos en partes más manejables.

Resuelve problemas de ecuaciones lineales usando métodos algebraicos adecuados .

Los números enteros son una parte importante de la matemática, y resolver problemas de ecuaciones lineales es una habilidad útil para tener. Para resolver estos problemas, hay que usar los métodos algebraicos adecuados. Esto significa que hay que seguir un conjunto de pasos para llegar a la solución correcta.

Primero, hay que identificar los términos en la ecuación y determinar si hay alguna incógnita. Después, hay que separar los coeficientes de las incógnitas y organizarlas en una matriz. A continuación, hay que multiplicar los coeficientes para obtener la solución correcta. Luego, hay que verificar si la solución es correcta utilizando los valores originales en la ecuación.

Para resolver problemas con números enteros usando métodos algebraicos adecuados se necesita práctica y dedicación. Con el tiempo, esto puede ayudar a mejorar las habilidades matemáticas y aumentar el conocimiento sobre los números enteros.

Estudia las leyes de los exponentes y cómo se relacionan con los números enteros .

Los números enteros son una parte importante de la matemática y estudiar las leyes de los exponentes es una parte fundamental para entenderlos. Los exponentes son una forma de escribir números multiplicados por sí mismos. Por ejemplo, el exponente «2» significa que el número se multiplica por sí mismo dos veces. Esto significa que 8^2 = 8 x 8 = 64.

Algunas leyes relacionadas con los exponentes también se aplican a los números enteros. Por ejemplo, la ley del producto dice que si dos expresiones tienen el mismo exponente, entonces el producto de estas expresiones tendrá el mismo exponente como resultado. Esta ley se aplica tanto a los enteros como a los decimales.

Por otro lado, la ley del cociente nos dice que si dos expresiones tienen el mismo exponente, entonces el cociente de estas expresiones tendrá un exponente igual al inverso del primer exponente. Esta ley también se aplica tanto a los enteros como a los decimales.

Es importante comprender cómo se relacionan las leyes de los exponentes con los números enteros para poder usarlas correctamente en problemas matemáticos más complejos. Estudiar y comprender estas leyes te ayudará a resolver problemas con mayor facilidad y eficacia en matemáticas y otros campos relacionados.

Practica la división sintética para dividir grandes cantidades por pequeñas cantidades en forma rápida y sencilla .

La división sintética es una herramienta útil para dividir grandes cantidades por pequeñas cantidades de manera rápida y sencilla. Esta técnica se basa en la división sucesiva y le permite al usuario dividir un número entero sin necesidad de realizar cálculos complicados. Esto puede ser especialmente útil cuando se trata de operaciones aritméticas básicas.

En primer lugar, el usuario debe identificar el divisor y el dividendo. Luego, el divisor se divide por el dividendo para obtener un cociente. A continuación, el cociente se multiplica por el dividendo para obtener un producto. Este producto se resta del dividendo original para obtener un residuo. El residuo se divide entonces por el divisor original para obtener un nuevo cociente, que se suma al anterior para obtener el resultado final.

La división sintética es una herramienta útil que puede ayudar a ahorrar tiempo y energía al realizar cálculos aritméticos básicos. Esta técnica simplifica la forma en que los números enteros se dividen entre sí, permitiendo a los usuarios completar sus cálculos de manera rápida y sencilla.